‘On Growth and Form’ and mathematical biology
Two students from the Mathematics Department, Heather Dickinson and Barbora Cernakova, recently undertook an internship, funded by the Strathmartine Trust, which involved consultation of the papers of Professor D’Arcy Wentworth Thompson. In this blog they highlight how Thompson’s ‘On Growth and Form’ led the way in the new area of study, mathematical biology.
This year we celebrate the centenary of the publication of D’Arcy Wentworth Thompson’s extraordinary book On Growth and Form.
D’Arcy Thompson was a Scottish polymath, excelling in topics as diverse as biology, mathematics and classics as well as being fluent in many languages. He was born in Edinburgh on 2nd May 1860 and studied at Edinburgh Academy from the age of 10. D’Arcy enrolled at Edinburgh University to study medicine in 1878 but moved to pursue zoology at Trinity College, Cambridge in 1880 and graduated Bachelor of Arts in Natural Science in 1883.
In 1884 D’Arcy was appointed Professor of Biology at the new University College, Dundee, a position he held for 32 years. Whilst in Dundee he set up a zoology museum which included specimens he collected on his voyages to the Bering Straits. These voyages were undertaken as part of an investigation into the fur seal industry and D’Arcy was one of the first people to push for conservation agreements. He was to spend the final 31 years of his life at St Andrews where he was appointed to the Chair of Natural History in 1917, the year in which his most important work was published. His record of holding a chair for 64 years is unlikely to be broken.
See more about D’Arcy’s life here.

D’Arcy is largely remembered for his work On Growth and Form, first published in 1917. The book is highly regarded not only for its unique material but also because of the way D’Arcy skilfully combined his knowledge of Biology and Maths with that of Literature and Languages. Indeed, there are untranslated passages in several languages including Latin, Greek, French, Italian and German.
D’Arcy hoped to encourage biologists to place more emphasis on mathematics and physics when explaining biological phenomena. A recurring theme throughout the book is that of the logarithmic spiral which can found all through nature from shells to horns. D’Arcy’s scientific approach to biology has inspired many scientists including Alan Turing, and led the way for a new area of study called mathematical biology. Scientists are still considering D’Arcy’s ideas and since the advent of the computer it has become easier to simulate and test some of them. Arguably the most famous chapter of On Growth and Form is chapter XVII named “On the Theory of Transformations, Or the Comparison of Related Forms”. In this chapter, D’Arcy explores to what extent related forms can be compared through simple mathematical transformations.

Special Collections is home to over 30,000 documents relating to D’Arcy, gifted to the University by his daughter Ruth. A small selection of these consist of correspondence with Danish artist and palaeontologist Gerhard Heilmann, who contributed both ideas and drawings to the transformation chapter. Upon realising that his transformation method was just what Heilmann required to advance his own work, D’Arcy introduced it to him through a “puzzle”. He drew a square grid onto which he drew a human skull, and another grid which had been deformed by bending or stretching the lines of the original. The challenge he posed for Heilmann was to project the image of the human skull onto this deformed grid. To Heilmann’s delight he recognised the new image to be that of a macaque (Macacus, a genus of Old World monkey).
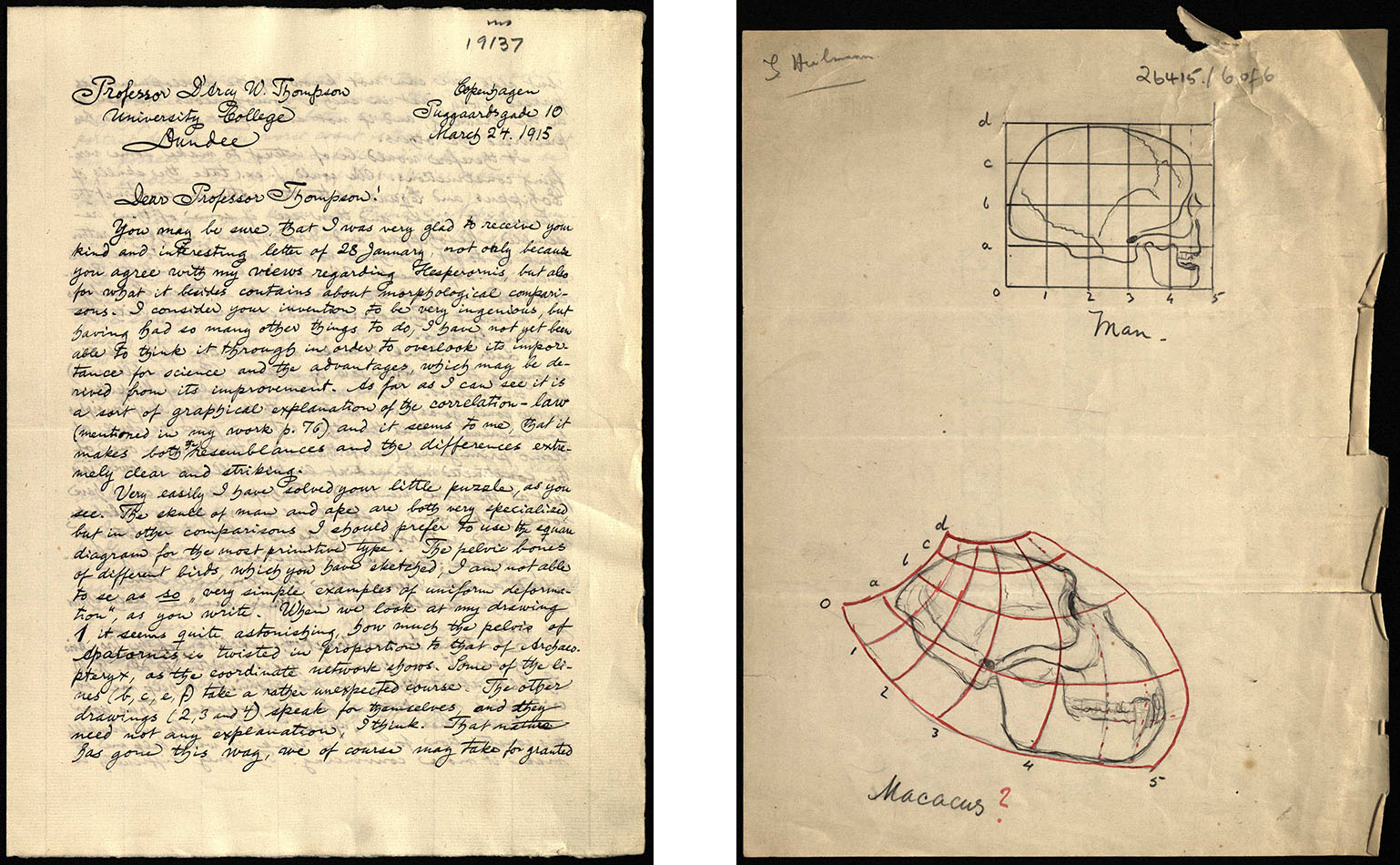
Heilmann saw the true potential of the transformation method. He realised that it could be used not only to transform one form into another but also to predict intermediate stages in evolutionary paths. After some experimentation, he decided that the Equidae family would demonstrate this beautifully.
Beginning with the skull of Eohippus (extinct genus of horses, donkeys and zebras), he was able to find a transformation which would produce the skull of Equus (modern genus of horses, donkeys, zebras). From detailed analysis of the required transformation he was able to break it down in stages, and from these stages deduce intermediate stages in the evolution of Eohippus to Equus. Heilmann was able to recognise Mesohippus (an extinct genus of early horse) and Protohippus (extinct three-toed genus of horse) amongst his predicted intermediate types. Interestingly, Parahippus, which was formerly believed to lie on the direct line of descent of Eohippus to Equus did not appear to fit. Heilmann assumed that Parahippus must belong to another stem of the Equidae. Indeed, , American palaeontologist Professor R S Lull confirmed Heilmann’s suspicions in his book Organic Evolution. This example provided strong evidence in favour of D’Arcy’s method.
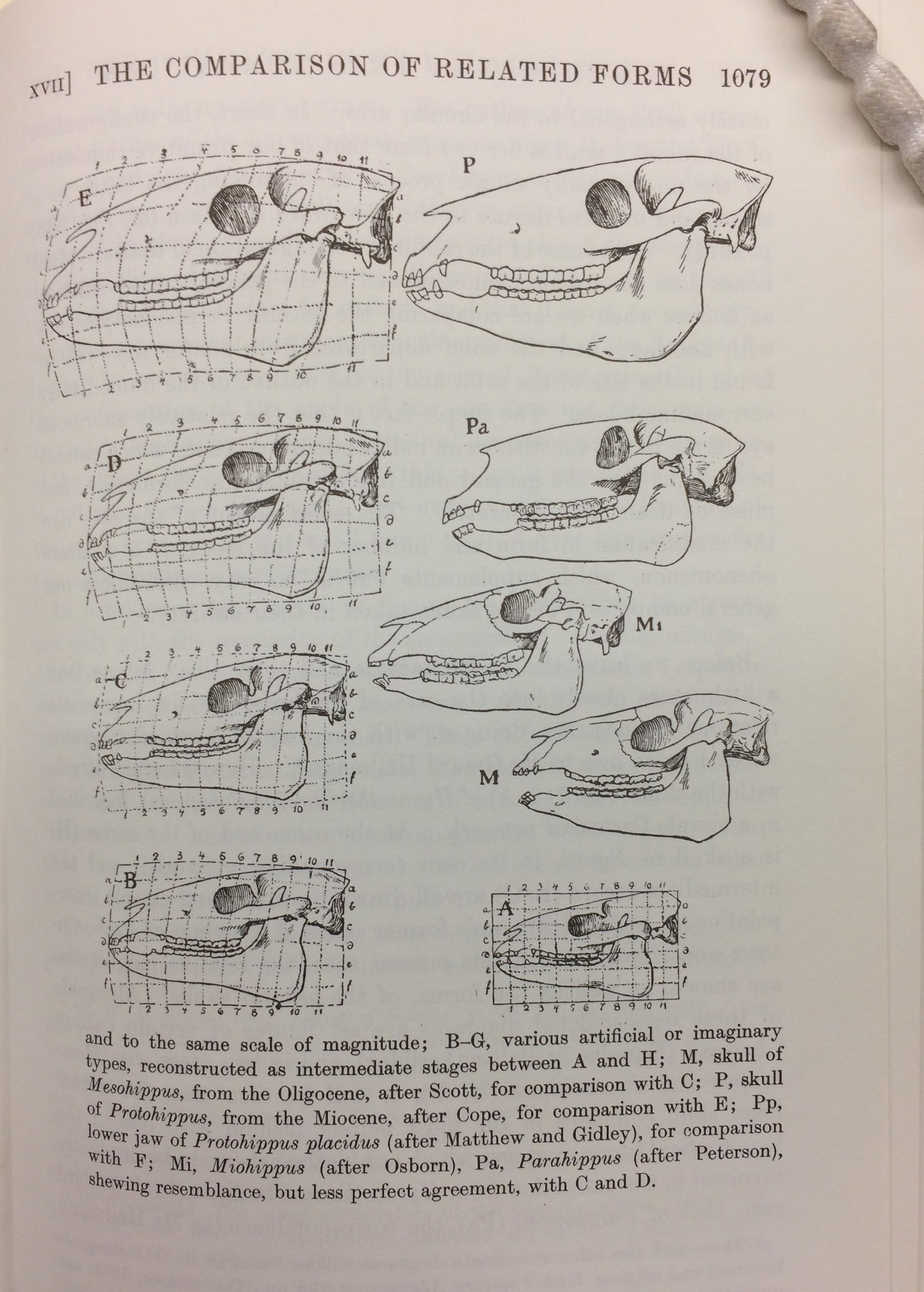
Transformation of Equidae skulls and comparison with known descendants
The two men realised that if the method could be used to predict intermediate stages it may also be possible to predict what unknown bones of dinosaurs may have looked like. By transforming from the pelvis bone of the well-known Stegosaurus D’Arcy was able to predict what a missing fragment of the pelvis bone of Camptosaurus may have looked like.
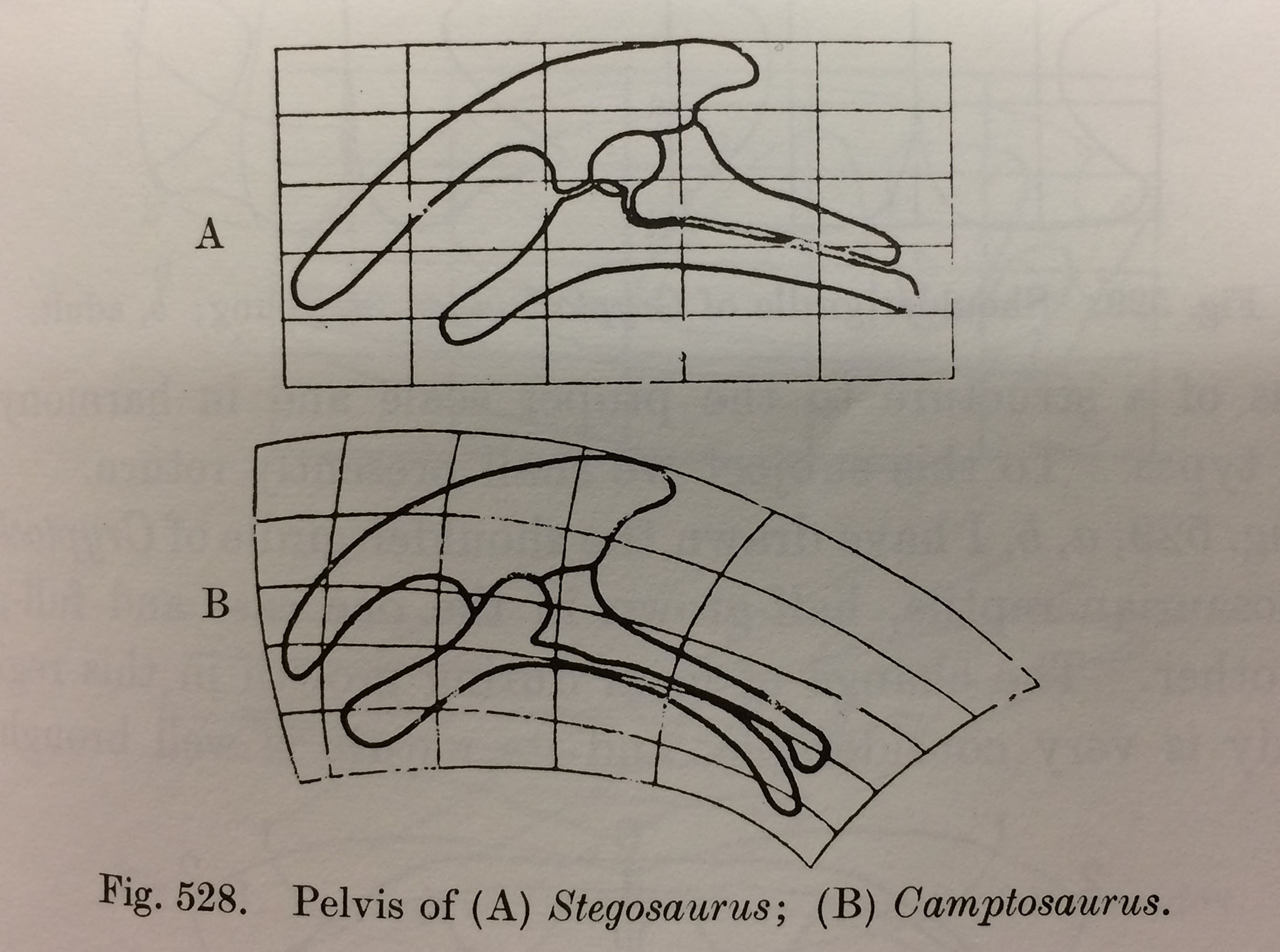
Transformation of Camptosaurus pelvis from Stegosaurus pelvis
Heilmann is just one example of the worldwide network of connections that D’Arcy cultivated, with whom he shared ideas and provided and drew inspiration, including other scientists, mathematicians, philosophers, classicists, artists and writers. The collection includes many of D’Arcy’s original notes and his own annotated copies of the first and second editions of On Growth and Form, letters from Charles Galton Darwin (grandson of famed naturalist Charles Darwin) on the wind deformation of trees (ms26399), discussion of whether Lilliputians are biologically feasible, ways to make the perfect tetrakaidekahedron with models made from card (ms28584, ms42744), papers on the British Association for the Advancement of Science, and letters from Julian Huxley, Geoffrey Thomas Bennet, George Greenhill, Dorothy Maud Wrinch, Sir Joseph Larmor, amongst so many others.
If you wish to find out more about the D’Arcy Thompson collection, visit the Special Collections’ website and search our online catalogue here.
See also these links on the upcoming conference in October to celebrate the 100th anniversary of the publication of On Growth and Form, and papers from the 150th anniversary of his birth in 2010.
https://www.ongrowthandform.org/conference/
https://www.ongrowthandform.org/
http://www.darcythompson.org/index.html
Society for Mathematical Biology: http://www.smb.org/history-of-the-society/
Heather Dickinson and Barbora Cernakova
Students in the Mathematics Department